Visual Basic Big Bang simulation program "VB BigBang.exe" and "VB2010 BigBang.exe"
Introduction and Purpose
The purpose of both programs is to demonstrate:
- The Big Bang as a simple linear model.
The model assumes that the speed of light is not influenced by the expanding space.
- The Big Bang as described by Milne's model .
The model assumes that the speed of light is a local concept and is influenced by the expanding space.
- That the expansion speed of space is a function of distance.
- That the observed age of a galaxy is a function of distance. How further away how younger.
- That the youngest observed galaxy is a function of expansion rate (multiple times c)
For a general introduction for both world models select this:
3 World models
For further reading read this: Misconceptions about the Big Bang
Execution file select: BIGBANG.ZIP
This zip file contains the files:
The program demonstrates the Big Bang over a period of 15 b years subdivided in periods of 1 b year by means of 150 galaxies or clocks. The 150 galaxies are randomly scatered over the Universe. The Observer is at the centre. Each billion Year is identified by a different colour.
Both program consists of 2 displays or forms: A Control Form and a Display Form
Control Form
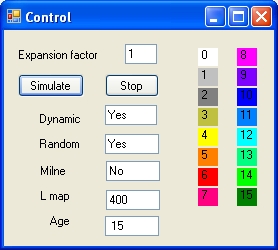
|
The picture on the left shows the control Form of the program "VB2010 BigBang.exe"
The display shows 4 input parameters: "Expansion Factor", "Dynamic" "Random""L map" and Milne 1 display parameter: "age" and 2 Buttons: "Simulate" and "End"
- The "Expansion Factor" shows the expansion factor of the universe. A value of 1 means the speed of light.
-
The parameter "Dynamic" when "Yes" shows the universe as a circle. When "No" as a square.
-
The parameter Random requires that the parameter "Dynamic" is "Yes".
When the parameter Random is "Yes" the angles of the galaxies are random.
When the parameter Random is "NO" the angles of the galaxies are calculated.
- The parameter "L map" allows you to resize the dimensions in pixels of the display form.
- The parameter Milne allows you to selct between the simple model and Milne
- The display parameter "age" shows the age of the universe.
- The "Simulate" Button is used start the simultion.
- The "End" Button is used to terminate the program.
|
When The "Simulate" Button is selected the "End" Button changes into the "Stop" Button
When the "Stop" Button is selected the simulation stops and the "Stop" Button changes into the "End" Button. The allows the user to modify the parameters and perform a second simulation
Operation
- First enter 1
- In the second run enter 3
- In the third run enter 0.3
- Finally enter 0 to end the program
Operation details simple linear model:
- An expansion factor of 1 means that the Universe expands with a speed of c. At the end of the demonstration, the simulation shows that the youngest galaxies you can see now are roughly 7.5 Billion year old and the oldest 15 Byear
- At the end of the simulation the total size of the universe is 15 B lightyears.
- An expansion factor of 2 means that the Universe expands with a speed of 2c. At the end of the demonstration, the simulation shows that the youngest galaxies you can see now are roughly 5 Byear old. That means you can see further back in time
- At the end of the simulation the total size of the universe is 30 B lightyears.
- With an expansion factor of 10, at the end of the simulation you will be able to see the state of the Universe very close at the moment of the Big Bang.
- With an expansion factor of 0.3, at the end of the demonstration, you will only see the galaxies between 12 and 15 Byears.
Display Form
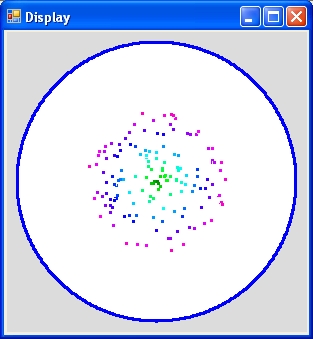
c = 1
|
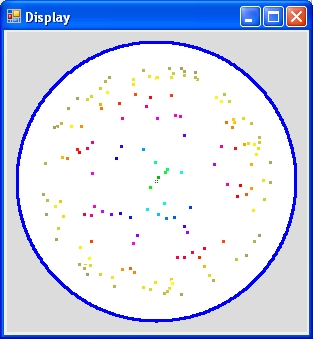
c = 5
|
- The display on the left shows the end of the simulation with c = 1
- The display on the right shows the end of the simulation with c = 5.
Both displays 150 galaxies. The distance between the galaxies is identical.The angles of the galaxies are random.
When you observe the left picture and when you compare that with the color table you will observe that the youngest galaxy at the rim of the universe is roughly 7 b years old.
For the right curve the age is much younger and roughly 1 b years old.
However what is much more remarkable that on the right picture there are much more younger galaxies than that are old galaxies. See also Reflection part 2.
D
/|
/ |
/ |
/ |
/ |
/ |
/ |
/ |
/ |
/ |
/ |
/ C
e / . |
. / . |
. / . |
d . |
/| . . |
/ | c A
/ | . | . . |
/ . | a |
/ . | . | . |
/ . . | | . |
/. . | | | . |
BB.......................O
0 5 8 11 15
Figure 1
|
The sketch left demonstrates how the program operates.
- Suppose that expansion factor is 2c.
- The line BB-O is the time axis t
- The line OACD is the x axis.
- The line BB-D represents is the line x=2t. This is the radius of the world model.
- The line BB-C represents the the path of a galaxy at a factor r from the radius with r between 0 and 1.
The line BB-C is represented by the equation x=2*r*t
- The line oacde is the linecone through O.
This line is represented in this case by x=15-t.
In general x=age-t
- The time of point d is calculated as 2t = 15 - t
or 3t = 15 or t = age/3
- The time of point c is calculated as 2rt = 15 - t
or 2rt + t = age or t = age /(2r+1)
- The distance of point c from the origin O is equal to
age - age/(2r+1) = 2r * age/(2r+1) in billion light years.
|
D
/|
/ |
/ |
/ |
/ |
/ |
/ |
/ |
/ |
/ |
/ |
/ C
e / . |
. / . |
. / . |
. . |
/ . . |
/ . |
/ . . |
/ c x x . |
d . | x x . |
x/|. | x x |
/.| | x |
BB.......................O
0 3 5 8 11 15
Figure 2
|
The sketch left demonstrates how the program operates.
- Suppose that expansion factor is 2c.
- The line BB-O is the time axis t
- The line OCD is the x axis.
- The line BB-D represents is the line x=2t. This is the radius of the world model.
- The line BB-C represents the the path of a galaxy at a factor r from the radius with r between 0 and 1.
The line BB-C is represented by the equation x=2*r*t
- The line O-e is the light cone through O.
This line is represented in this case by x=15-t.
- The blue line through the points D and X is the path of a light ray from the Big Bang to the observer at O.
The line is implemented as a table. The first billion years is implemented in 40 segments and the part between 1 b years and 15 b years in 14 segments.
Each line segment is described by the function a+bt.
To calculate the time of point x the following equation has to be solved: a+bt = 2rt
or t = a / (2r-b)
- The distance of point c = age - t in billion light years
|
Reflection part 1. Simple linear model versus Milne's model
- First perform a simulation with the following parameter settings:
"Expansion Factor" = 1 "Dynamic" = Yes "Random" = Yes and Milne = No.
- When the simulation is done select the Milne = Yes parameter a couple of times. You will see a small change in the colours.
- Next select the Random = Yes parameter once and like above select the Milne parameter a couple of times. You will again see a small change in the colours.
- Next change the "Expansion Factor" to 3 and like before select the Milne parameter a couple of times. (with either the "Random" = Yes or No.
What you will observe is that when the Milne parameter is Yes you can observe much younger galaxies.
- When you try expansion factor to 5 you will observe small white dots at the blue rim of the Universe. That means you can observe the Big Bang with the Milne Universe.
It should be remembered that the current cosmological are close to an expansion factor of 3. See: 3 World models
Reflection part 2. Simple linear model versus Milne's model
When you perform a simulation with higher expansion factors you will observe that there are much more galaxies at the outside than on the inside.
When you observe Figure 1 the youngest galaxy you can observe is roughly 5 b years old (With expansion factor 2). This is the point d in the line Oacde
The line BB-C represents expansion factor of 1. That line crosses the line Oe at point c. The exact age of that point is 7.5 b years old.
The simulation is based on the phylosophy that the universe is homogeous and uniform. That means in the vertical line DCAO the number of galaxies in the segment DC is identical as in the segment CAO.
For the line Oacde this is the same. The number of galaxies in dc is identical as in caO.
This explains why there are more galaxies in the outer segment than in the inner segment.
In Figure 2, the Milne's model, the same situation exists and because with an expansion factor of 3 the Milne model is almost identical as the present situation it should also be possible to test this by observing the sky.
This phenomena can the best be viewed by setting the Random parameter to "No".
Feedback
None
Created: 5 Februari 2014
Back to my home page: Contents of This Document


